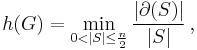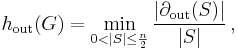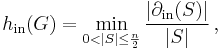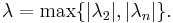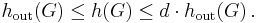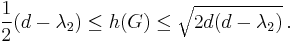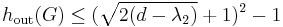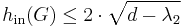Expander graph
In combinatorics, an expander graph is a sparse graph that has strong connectivity properties, quantified using vertex, edge or spectral expansion as described below. Expander constructions have spawned research in pure and applied mathematics, with several applications to complexity theory, design of robust computer networks, and the theory of error-correcting codes.[1]
Contents |
Definitions
There are several different ways to measure the expansion properties of a finite, undirected multigraph  .
.
Edge expansion
The edge expansion (also isoperimetric number or Cheeger constant) 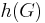 of a graph
of a graph  is defined as
is defined as
where the minimum is over all nonempty sets  of at most
of at most 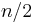 vertices and
vertices and 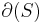 is the edge boundary of
is the edge boundary of  , i.e., the set of edges with exactly one endpoint in
, i.e., the set of edges with exactly one endpoint in  .[2]
.[2]
Vertex expansion
The vertex isoperimetric number 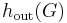 (also vertex expansion or magnification) of a graph
(also vertex expansion or magnification) of a graph  is defined as
is defined as
where 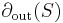 is the outer boundary of
is the outer boundary of  , i.e., the set of vertices in
, i.e., the set of vertices in 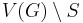 with at least one neighbor in
with at least one neighbor in  .[3] In a variant of this definition (called unique neighbor expansion)
.[3] In a variant of this definition (called unique neighbor expansion) 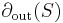 is replaced by the set of vertices in
is replaced by the set of vertices in  with exactly one neighbor in
with exactly one neighbor in  .
.
The vertex isoperimetric number 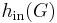 of a graph
of a graph  is defined as
is defined as
where 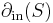 is the inner boundary of
is the inner boundary of  , i.e., the set of vertices in
, i.e., the set of vertices in  with at least one neighbor in
with at least one neighbor in 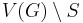 .[3]
.[3]
Spectral expansion
When  is regular, a linear algebraic definition of expansion is possible based on the eigenvalues of the adjacency matrix
is regular, a linear algebraic definition of expansion is possible based on the eigenvalues of the adjacency matrix 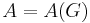 of
of  (where
(where 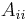 is the number of loops at the
is the number of loops at the  th vertex).[4] Because
th vertex).[4] Because  is symmetric, the spectral theorem implies that
is symmetric, the spectral theorem implies that  has
has  real-valued eigenvalues
real-valued eigenvalues 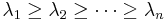 . Because
. Because  is regular,
is regular, 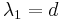 where
where  is the degree of vertices of
is the degree of vertices of  . In some contexts, the spectral gap of
. In some contexts, the spectral gap of  is defined to be
is defined to be 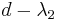 . In other contexts, the spectral gap is
. In other contexts, the spectral gap is 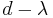 , where
, where
The normalized version of this definition, where we consider the matrix 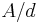 and get eigenvalues between −1 and 1, is also widely used and more convenient in the statement of some results.
and get eigenvalues between −1 and 1, is also widely used and more convenient in the statement of some results.
Frequently one will refer to the second-largest eigenvalue of a graph G, which is the max of 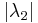 and
and 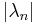 . Depending on the context it may be either the normalized version (taking value between 0 and 1) or the un-normalized version (taking value between 0 and d).
. Depending on the context it may be either the normalized version (taking value between 0 and 1) or the un-normalized version (taking value between 0 and d).
For not necessarily regular graphs, the spectrum of a graph can be defined similarly using its Laplacian matrix.
Expander families
A family 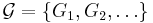 of
of  -regular graphs is an edge expander family if there is a constant
-regular graphs is an edge expander family if there is a constant 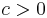 such that
such that 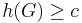 for each
for each 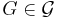 . Typically we want
. Typically we want  to be constant, though it is sometimes also interesting to consider
to be constant, though it is sometimes also interesting to consider 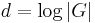 or even
or even 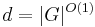 . Similarly,
. Similarly, 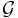 is a vertex expander family if there is a constant
is a vertex expander family if there is a constant 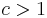 such that
such that 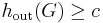 for each
for each 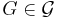 , and
, and 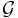 is a spectral expander family if some positive constant is a lower bound for the spectral gap of each
is a spectral expander family if some positive constant is a lower bound for the spectral gap of each 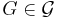 .
.
These definitions can be extended to the case of directed graphs. A directed graph can also be interpreted as a balanced bipartite graph (with all edges going from one copy of  to another copy). The definition of bipartite expanders can further be generalized to the case of unbalanced bipartite graphs.
to another copy). The definition of bipartite expanders can further be generalized to the case of unbalanced bipartite graphs.
Relationships between different expansion properties
The expansion parameters defined above are related to each other. In particular, for any  -regular graph
-regular graph  ,
,
Consequently, for constant degree graphs, vertex and edge expansion are qualitatively the same.
Cheeger inequalities
When  is
is  -regular, there is a relationship between
-regular, there is a relationship between 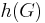 and the spectral gap
and the spectral gap 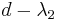 of
of  . An inequality "due to Cheeger and Buser in the continuous case and to Tanner, Alon, and Milman in the discrete case"[5] states that
. An inequality "due to Cheeger and Buser in the continuous case and to Tanner, Alon, and Milman in the discrete case"[5] states that
This inequality is closely related to the Cheeger bound for Markov chains and can be seen as a discrete version of Cheeger's inequality in Riemannian geometry.
Similar connections between vertex isoperimetric numbers and the spectral gap have also been studied:[7]
Asymptotically speaking, the quantities 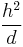 ,
, 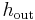 , and
, and 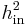 are all upper bounded by the spectral gap
are all upper bounded by the spectral gap 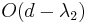 .
.
Examples of expanders
A random  -regular graph has good expansion, with high probability. Ramanujan graphs are a family of
-regular graph has good expansion, with high probability. Ramanujan graphs are a family of  -regular expander graphs with
-regular expander graphs with  being constant and with explicit constructions, that have essentially the largest possible spectral gap. Algebraic constructions based on Cayley graphs are known for various variants of expander graphs. Most recently, combinatorial constructions of expanders have also been discovered.
being constant and with explicit constructions, that have essentially the largest possible spectral gap. Algebraic constructions based on Cayley graphs are known for various variants of expander graphs. Most recently, combinatorial constructions of expanders have also been discovered.
Applications and useful properties
The original motivation for expanders is to build economical robust networks (phone or computer): an expander with bounded valence is precisely an asymptotic robust graph with number of edges growing linearly with size (number of vertices), for all subsets.
Expander graphs have found extensive applications in computer science, in designing algorithms, error correcting codes, extractors, pseudorandom generators, sorting networks (Ajtai, Komlós & Szemerédi (1983)) and robust computer networks. They have also been used in proofs of many important results in computational complexity theory, such as SL=L (Reingold (2008)) and the PCP theorem (Dinur (2007)). In cryptography, expander graphs are used to construct hash functions.
The following are some properties of expander graphs that have proven useful in many areas.
Expander mixing lemma
The expander mixing lemma states that, for any two subsets of the vertices 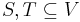 , the number of edges between
, the number of edges between  and
and  is approximately what you would expect in a random
is approximately what you would expect in a random  -regular graph, i.e.
-regular graph, i.e. 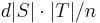 .
.
Expander walk sampling
The Chernoff bound states that, when sampling many independent samples from a random variables in the range ![[-1, 1]](/2012-wikipedia_en_all_nopic_01_2012/I/d060b17b29e0dae91a1cac23ea62281a.png) , with high probability the average of our samples is close to the expectation of the random variable. The expander walk sampling lemma, due to Ajtai, Komlós & Szemerédi (1987) and Gillman (1998), states that this also holds true when sampling from a walk on an expander graph. This is particularly useful in the theory of derandomization, since sampling according to an expander walk uses much fewer random bits than sampling independently.
, with high probability the average of our samples is close to the expectation of the random variable. The expander walk sampling lemma, due to Ajtai, Komlós & Szemerédi (1987) and Gillman (1998), states that this also holds true when sampling from a walk on an expander graph. This is particularly useful in the theory of derandomization, since sampling according to an expander walk uses much fewer random bits than sampling independently.
See also
Notes
- ^ Hoory, Linial & Widgerson (2006)
- ^ Definition 2.1 in Hoory, Linial & Widgerson (2006)
- ^ a b Bobkov, Houdré & Tetali (2000)
- ^ cf. Section 2.3 in Hoory, Linial & Widgerson (2006)
- ^ See [1]
- ^ Theorem 2.4 in Hoory, Linial & Widgerson (2006)
- ^ Theorem 1 in Bobkov, Houdré & Tetali (2000)
References
Textbooks and surveys
- Chung, Fan R. K. (1997), Spectral Graph Theory, CBMS Regional Conference Series in Mathematics, 92, American Mathematical Society, ISBN 0-8218-0315-8
- Davidoff, Guiliana; Sarnak, Peter; Valette, Alain (2003), Elementary number theory, group theory and Ramanjuan graphs, LMS student texts, 55, Cambridge University Press, ISBN 0-521-53143-8
- Hoory, Shlomo; Linial, Nathan; Widgerson, Avi (2006), "Expander graphs and their applications", Bulletin (New series) of the American Mathematical Society 43 (4): 439–561, doi:10.1090/S0273-0979-06-01126-8, http://www.cs.huji.ac.il/~nati/PAPERS/expander_survey.pdf
Research articles
- Ajtai, M.; Komlós, J.; Szemerédi, E. (1983), "An O(n log n) sorting network", Proceedings of the 15th Annual ACM Symposium on Theory of Computing, pp. 1–9, doi:10.1145/800061.808726
- Ajtai, M.; Komlós, J.; Szemerédi, E. (1987), "Deterministic simulation in LOGSPACE", Proceedings of the 19th Annual ACM Symposium on Theory of Computing, pp. 132–140, doi:10.1145/28395.28410
- Bobkov, S.; Houdré, C.; Tetali, P. (2000), "λ∞, vertex isoperimetry and concentration", Combinatorica 20 (2): {153--172, doi:10.1007/s004930070018}.
- Dinur, Irit (2007), "The PCP theorem by gap amplification", Journal of the ACM 54 (3): 12, doi:10.1145/1236457.1236459.
- Gillman, D. (1998), "A Chernoff Bound for Random Walks on Expander Graphs", SIAM Journal on Computing (Society for Industrial and Applied Mathematics) 27 (4,): 1203–1220, doi:10.1137/S0097539794268765
- Reingold, Omer (2008), "Undirected connectivity in log-space", Journal of the ACM 55 (4): Article 17, 24 pages, doi:10.1145/1391289.1391291